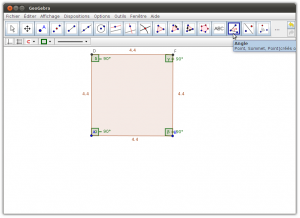
Mesurer des angles, calculer un périmètre ou une aire posent des contraintes importantes pour l’élève ayant des difficultés de motricité fine. Pour ces élèves il est difficile d’acquérir ces notions puisque la manipulation d’outils conventionnels tels que l’équerre, le compas, la règle ou le rapporteur d’angle s’avère difficile voire impossible. Toutefois, plusieurs logiciels permettent la manipulation virtuelle de ces outils.
1. Tableau comparatif de logiciels permettant l’utilisation d’un rapporteur d’angles virtuel
- Introduction au tableau (format PDF)
- Tableau comparatif des rapporteurs d’angles virtuels (format PDF)
2. Avec Instrumenpoche
Instrumenpoche est un logiciel spécialement conçu pour l’élève ayant une déficience motrice. Il offre différents outils permettant de tracer des figures géométriques.
3. Avec Trousse Géo Tracée (TGT)
La trousse TGT permet de réaliser des tracés de géométrie avec manipulation d’outils virtuels. Elle a été conçue pour les élèves ayant une déficience motrice.
4. Avec ToutEnClic
Ce logiciel permet à l’élève d’utiliser des outils virtuels sur des documents numérisés. Il a été conçu pour les élèves ayant une déficience motrice cependant, on constate certaines limites d’utilisation.
5. Avec Notebook
Notebook, logiciel de présentation attaché au tableau numérique tactile SmartBoard contient certains outils virtuels pouvant être utilisés pour des tracés géométriques.
6. Avec Sankoré
Sankoré est un logiciel de présentation attaché au tableau numérique tactile qui contient certains outils virtuels pouvant être utilisés pour des tracés géométriques.