Le logiciel BOMEHC s’adresse non seulement aux élèves mais aussi au corps professoral. En effet, il intègre une interface spécialement conçue pour les enseignants. Ils peuvent ainsi activer ou désactiver des fonctions précises et peuvent l’utiliser de manière efficace dans tous les types de configuration pédagogique (phase de cours, d’exercices et d’applications et aussi phases de tests ou contrôles).
Le logiciel BOMEHC s’adresse non seulement aux élèves mais aussi au corps professoral. En effet, il intègre une interface spécialement conçue pour les enseignants. Ils peuvent ainsi activer ou désactiver des fonctions précises et peuvent l’utiliser de manière efficace dans tous les types de configuration pédagogique (phase de cours, d’exercices et d’applications et aussi phases de tests ou contrôles).
Pour atteindre les objectifs du projet (logiciel complet, simple d’utilisation, intuitif), plusieurs idées innovantes ont été mises en place :
La première est la séparation de la fenêtre du logiciel en deux :
- La partie gauche contient le Traitement de texte dans lequel il est possible de saisir du texte et des formules mathématiques de façon simple.
- Et la partie droite est réservée aux travaux pratiques, comme les tracés géométriques, les tableaux de proportionnalité, les fonctions, ou encore les opérations.
Ainsi l’élève peut travailler sur la partie droite tout en regardant son cours ou l’énoncé de l’exercice sur la partie gauche.

La partie Traitement de texte est composée de trois onglets : le cahier de cours, le cahier d’exercices, et le cahier de brouillon. Il s’agit d’un traitement de texte volontairement simplifié, permettant de saisir des formules mathématiques grâce à un clavier virtuel qui offre la possibilité d’écrire des formules complexes en seulement quelques clics.
Il est également possible d’y insérer les travaux réalisés dans la partie travail pratique (partie droite). L’élève peut donc illustrer son cours par de nombreux exercices qu’il pourra, par la suite, éditer afin de les corriger ou de les retravailler.

La partie Travail Pratique est constituée de quatre onglets :
- Onglet Opérations : Il permet de poser toutes les opérations (additions, soustractions, multiplications et divisions) de la même façon que sur un cahier. Il s’agit pour l’élève d’un outil d’aide à la mise en forme et non de correction automatique de ses erreurs, ceci afin de lui permettre de se tromper et de bénéficier de la correction de l’enseignant.

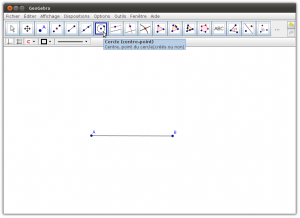
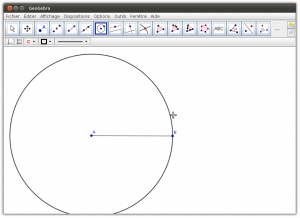
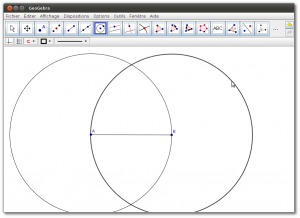
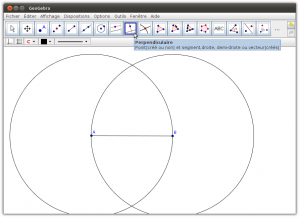
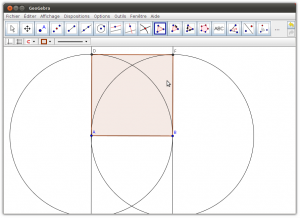
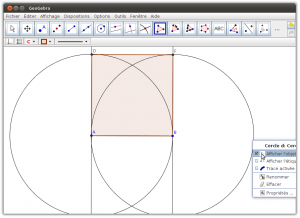
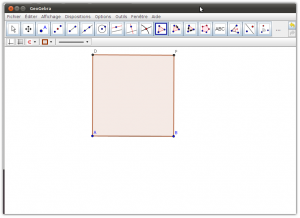
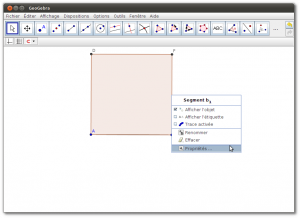
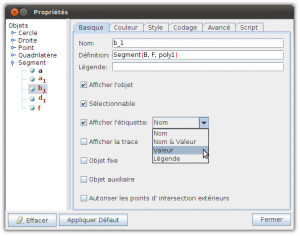
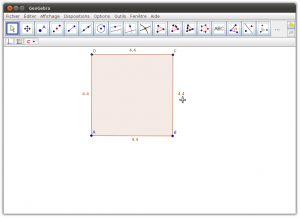
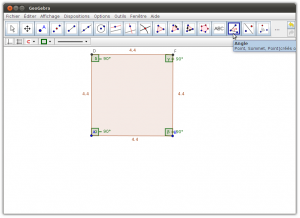
- Onglet Géométrie : Il permet de tracer des figures géométriques (points, segments, droites, demi-droites, arcs de cercles…), avec la possibilité d’afficher un repère et un quadrillage. Cette partie fournit uniquement les outils de base pour construire les figures, pour que l’élève suive les mêmes étapes que lors de la construction sur un cahier (tracés au compas, …). En fonction des actions de l’élève, le logiciel va guider ses tracés pour lui permettre de réaliser ce qu’il souhaite en seulement quelques clics intuitifs.

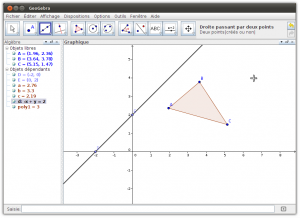
- Onglet Fonctions : Il offre la possibilité de tracer des courbes dans un repère. On peut par exemple tracer une fonction affine à partir de deux points, tracer des points et les relier par des segments pour approcher une fonction, ou encore dessiner une courbe passant par plusieurs points pour imiter l’action d’un élève qui tracerait à la main une courbe.

- Onglet Tableaux : Il permet de créer un tableau simplement, de le remplir, d’ajouter ou de supprimer des colonnes/lignes, de colorier des cases, et de placer des flèches de proportionnalité entre des colonnes/lignes. Cet outil est notamment utilisé en statistique et en proportionnalité (règle de trois).
Comme il s’agit d’un logiciel libre, le logiciel et son code source sont accessibles, et vous pouvez dès maintenant tester le logiciel (même s’il n’est pas terminé) et participer au projet en laissant des idées, remarques, ou conseils aux créateurs.
Le logiciel BOMEHC n’a pas pour but de rivaliser avec les performances des autres logiciels de mathématiques. Son objectif est au contraire d’être très simple, mais complet. Il a surtout pour ambition d’avoir été conçu en partant des besoins des élèves en situation de handicaps divers. Ainsi, sa simplicité et son ergonomie intuitive le rendent beaucoup plus accessible que d’autres logiciels de mathématiques.
Poser une addition…