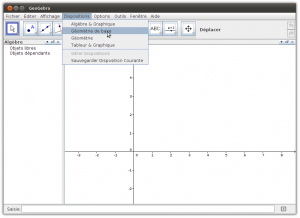
Math Paper est une application mobile IPAD (payante: 19,99$) dédiée à des élèves qui éprouvent des difficultés marquées de motricité fine.
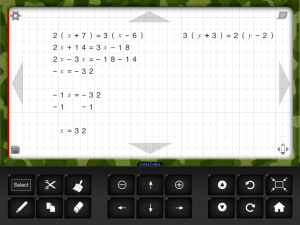
Il s’agit d’une application qui permet de réaliser des opérations mathématiques simples (addition, soustraction, division, multiplication, fractions) et des opérations algébriques simples.
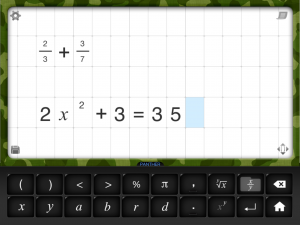
L’outil facilite l’édition des opérations et équations en offrant un clavier accessible en bas de l’écran et en proposant des boutons d’édition qui facilitent la saisie de données en réduisant le nombre de sélections dans l’écran. Pour certaines opérations mathématiques, le curseur se déplace automatiquement sur la case suivante ou sur la case anticipée (ex: lors d’une addition, une fois le premier chiffre indiqué, s’il y a lieu, le curseur se positionne sur la case de retenue.)
L’élève dispose de fichiers de travail comportant une grille qui facilite la saisie des données. On peut modifier la grosseur des cases pour faciliter la sélection des cases et l’entrée de données. L’outil est facilitant pour des élèves qui ont des difficultés d’organisation spatiale.
Différents modes de flèches à l’écran ou au clavier facilitent le déplacement dans la page et le déplacement du curseur. L’outil comporte un module pour éditer un problème mathématique à résoudre. La question devient accessible à l’élève par un clic sur l’onglet. S’ouvre alors un ruban où apparaît la question. Ce ruban peut être refermé pour libérer la surface de travail.
Il est possible de sauvergarder les fichiers de travail de l’élève et de créer des dossiers. Le partage des fichiers est également disponible en mode PDF ou en fichiers de format MathPaper utilisable par tout utilisateur de l’application.
Pour en savoir plus sur le produit développé par Panther Technology