Voici la vidéo de la construction d’un carré (méthode proposée)
Si vous avez des problèmes avec le vidéo, voici une alternative:
Cliquer sur l’image pour l’agrandir
Commentaires fermés sur Vidéo Construire un carré avec GeoGebra
Publié dans Besoins ciblés
Mots-clés : construire, géométrie, mathématique, tracer
Voici une méthode mathématique simple de construction d’un carré.
1. Démarrer GeoGebra.
2. Dans le menu «Dispositions», sélectionner «Géométrie de base»
3. Vous obtenez la fenêtre ci-dessous
4. Créer deux points dans le plan
Cliquer l’outil «Nouveau point»
Cliquer dans le plan afin de créer les deux points A et B
5. Créer un segment entre ces deux points
Cliquer sur l’outil «Segment entre deux points»
Tracer le segment en cliquant sur A et par la suite B
6. Créer un cercle de centre A et ayant comme extrémité de rayon B
Cliquer sur l’outil «Cercle (centre-point)»
Cliquer sur le point A et par la suite sur le point B
7. Créer un cercle de centre B et ayant comme extrémité de rayon A
Cliquer sur le point B et par la suite sur le point A
8. Tracer une droite perpendiculaire au segment AB passant par A
Cliquer sur l’outil «Perpendiculaire»
Cliquer sur le segment AB et, par la suite, sur le point A (perpendiculaire passant par A)
9. Tracer une droite perpendiculaire au segment AB passant par B
Cliquer sur le segment AB et, par la suite, sur le point B (perpendiculaire passant par B)
10. Créer un point d’intersection entre le cercle de centre A avec la perpendiculaire passant par A
Cliquer sur l’outil «Intersection entre deux objets»
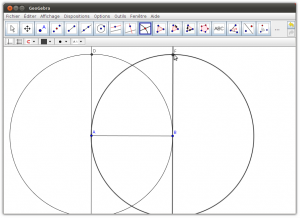
Cliquer sur le cercle de centre A et, par la suite, cliquer sur la perpendiculaire passant par A (deux points vont apparaître aux deux endroits où la perpendiculaire coupe le cercle A)
11. Créer un point d’intersection entre le cercle de centre B avec la perpendiculaire passant par B
Cliquer sur le cercle de centre B et, par la suite, cliquer sur la perpendiculaire passant par B (deux points vont apparaître aux deux endroits où la perpendiculaire coupe le cercle B)
12. Créer un polygone en reliant les points A, B, D et F (il est possible que les points d’intersection ne se nomment pas D et F)
Cliquer sur l’outil «Polygone»
Relier les points (revenir au point de départ pour fermer le polygone)
13. Cacher les traces de construction. Conserver seulement le polygone créé soit un carré.
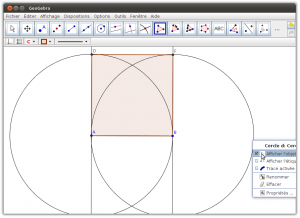
Cliquer le bouton droit sur l’objet à cacher. Cliquer sur «Afficher l’objet» afin d’enlever le crochet
Cacher tous les objets sauf le polygone.
Résultat possible
14. Faire afficher la mesure des segments composant le polygone.
Cliquer le bouton droit sur un des côtés du polygone et sélectionner «Propriétés»
Pour chaque segment composant le polygone, faire afficher la valeur de celui-ci
Résultat possible
15 Faire afficher la mesure des angles internes.
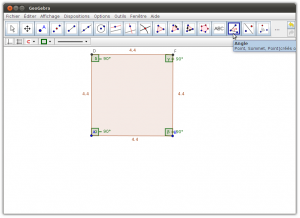
Cliquer sur l’outil «Angle» et cliquer à l’intérieur de votre polygone. La mesure des angles s’affichera.
Nous avons maintenant un véritable carré au sens mathématique du terme. En déplaçant les points A et B, le polygone créé conserve ses propriétés. Afin d’en connaître un peu plus sur le carré, visitez Wikipédia.
Commentaires fermés sur Construire un carré (méthode)
Publié dans Besoins ciblés
Mots-clés : géométrie, handicap, mathématique, motricité, tracer
Résumé
Rapporteur (le logiciel) permet de s’entraîner à l’utilisation du rapporteur (l’instrument). Il s’adresse à des élèves de primaire ou du secondaire.
Deux types d’activités sont proposées :
Les mesures d’angles sont générées aléatoirement (entre 5 et 175°).
Trois essais sont possibles, par exercice.
L’enseignant peut paramétrer :
Installation du logiciel
Configuration
Windows 95 ou supérieur, 1 Mo d’espace disque.
Licence
Rapporteur est un gratuiciel (utilisation libre et gratuite).
Téléchargement
| Fichier | Taille | Date | Description |
|---|---|---|---|
| rappo_setup.exe | 522 Ko | Juin 2004 | Rapporteur (Juin 2004) |
Exemple d’utilisation: Mesurer un angle avec Rapporteur
Rapporteur sert à apprendre à mesurer et à tracer des angles. Il offre à l’utilisateur de manipuler virtuellement un rapporteur d’angle et un crayon.
Dans le menu « Exercice », si vous sélectionnez « Mesurer un angle »
vous serez en mode d’apprentissage de la mesure d’un angle. Les mesures d’angles sont générées aléatoirement (entre 5° et 175°).
La boîte à outils
Après avoir placé le rapporteur pour effectuer la mesure, vous inscrivez le résultat dans la case de la boîte à outils:
et cliquez par la suite sur le bouton à droite qui permettra de vérifier votre réponse.
Vous avez 3 essais afin de réussir la tâche.
Les autres boutons composant la boîte à outils:
Quelques réglages
Via le fichier Rappo.ini qui se retrouve dans le répertoire du logiciel
[NbEx/Serie]
Mesurer=10 ->nombre d’exercices par série (10 par défaut)
Tracer=10 ->nombre d’exercices par série (10 par défaut)
[Angle]
SommetAimante=1 -> sommet de l’angle aimanté (oui(1) par défaut)
CoteHorizontal=0 -> un côté de l’angle horizontal (non par défaut)
Vidéo de cet exemple
Autre exemple d’utilisation: Tracer un angle avec Rapporteur
Rapporteur sert à apprendre à mesurer et à tracer des angles. Il offre à l’utilisateur de manipuler virtuellement un rapporteur d’angle et un crayon.
Dans le menu « Exercice », si vous sélectionnez « Tracer un angle »
vous serez en mode d’apprentissage du traçage d’un angle. Les mesures d’angles sont générées aléatoirement (entre 5° et 175°).
La boîte à outils
Après avoir placé le rapporteur pour tracer la mesure, vous cliquez sur l’outil crayon de la boîte à outils:
et tracez avec le crayon l’angle souhaité. Cliquez par la suite sur le bouton qui permettra de vérifier votre réponse.
Vous avez 3 essais afin de réussir la tâche.
Les autres boutons composant la boîte à outils:
Quelques réglages
Via le fichier Rappo.ini qui se retrouve dans le répertoire du logiciel
[NbEx/Serie]
Mesurer=10 ->nombre d’exercices par série (10 par défaut)
Tracer=10 ->nombre d’exercices par série (10 par défaut)
[Angle]
SommetAimante=1 -> sommet de l’angle aimanté (oui(1) par défaut)
CoteHorizontal=0 -> un côté de l’angle horizontal (non par défaut)
Vidéo de cet exemple
Les savoirs essentiels liés au programmes de formation
À la fin du 3e cycle au primaire, l’élève devrait être capable de mesurer et d’estimer un angle.
Angles : estimation et mesurage
Au secondaire, il doit réinvestir ces notions afin de les réutiliser dans des contextes de résolution de problèmes. Certains savoirs nécessitent l’utilisation de l’outil.
Commentaires fermés sur Rapporteur
Publié dans Logiciels d'apprentissage du domaine
Résumé
Toutenclic permet de travailler à l’écran sur un document numérisé, de la même façon que sur un cahier. L’enseignant numérise la fiche de travail, puis il l’importe avec Toutenclic. Ensuite, l’élève peut travailler à l’écran en utilisant toute une palette d’outils correspondant aux consignes les plus courantes : écrire, souligner, barrer, entourer, colorier, déplacer, mesurer …
Toutenclic permet d’importer des fiches de travail préalablement numérisée dans l’un des formats suivants : jpeg, png, gif, bmp.
Une fois importée, la fiche apparaît à l’écran et l’élève a à sa disposition une collection d’outils pour travailler « par dessus ». On peut :
Pour chaque outil, il est possible de spécifier l’épaisseur du trait et le taux de transparence : on peut ainsi, par exemple, simuler l’utilisation d’un surligneur (qui laisse voir ce qui est dessous).
Toutes les actions peuvent être annulées, le travail peut être sauvegardé et imprimé.
Note: Le texte de description est tiré du site Framasoft:
http://www.framasoft.net/article4908.html
Installation du logiciel
Configuration nécessaire
Voici les indications de l’auteur:
Les dépendances du programme
Pour pouvoir fonctionner ToutEnClic nécessite la présence, sur le poste sur lequel il est installé, de l’interpréteur python, des bibliothèques wxPython, python imaging et python-reportlab.
À noter que sur Ubuntu, il suffit d’installer les paquets python-wxgtk2.8, python-reportlab et python-imaging via synaptic pour que toutes les dépendances soient résolues.
Installation sous GNU/Linux
Si toutes les dépendances du programmes sont installées sur la machine, il suffit d’extraire le répertoire de l’archive tar.gz du source, récupérée en zone de téléchargement , et de le placer sous votre répertoire utilisateur.
Le fichier toutenclic.py situé à la racine de ce répertoire est un script exécutable, et double-cliquer dessus lancera l’application.
Installation sous Windows 32 bits
À partir des sources
Il vous faudra installer toutes les dépendances requises en les téléchargeant depuis les sites officiels indiqués ci-dessus, puis récupérer l’archive .zip du programme source en zone de téléchargement et l’extraire sous votre répertoire habituel de travail.
Un double-clic sur le fichier toutenclic.py lancera l’application. Cependant, une fenêtre DOS apparaîtra lors du lancement. Pour éviter cela, renommer le fichier toutenclic.py en toutenclic.pyw. Le programme se lancera alors en mode autonome.
À partir d’un exécutable
Devant la difficulté rencontrée par certains utilisateurs pour installer toutes les dépendances, l’auteur s’est résigné à créer un exécutable autonome.
Récupérer l’archive .zip en zone de téléchargement, en extraire le répertoire toutenclic-« version »-win32, et il suffit alors de double-cliquer sur l’exécutable toutenclic.exe situé à sa racine pour que cela fonctionne…
Licence
ToutenClic est un logiciel OpenSource développé par Alain DELGRANGE
Copyright © 2009 – 2011 Alain DELGRANGE aka bipede
http://www.bipede.fr/contrib/
Licence GNU-GPL version 2
Téléchargement
Vous trouverez le tout sur la page de téléchargement de ToutenClic
Utilisation en classe
Toutenclic permet à l’élève qui ne peut manipuler des instruments de mesure tels la règle, le rapporteur d’angle, l’équerre ou le compas, de disposer de ces outils numériques pour réaliser plus facilement les tâches mathématiques à l’ordinateur. Il s’agit alors de rendre l’activité mathématique en format numérique selon les spécifications du logiciel afin de permettre à l’élève d’utiliser les outils de mesure. L’élève sélectionne alors son outil, par exemple, le rapporteur d’angle, qui se superpose sur la feuille numérique. Il déplace l’outil pour ensuite effectuer sa mesure à l’endroit désiré. Il peut laisser des traces de son travail et l’imprimer par la suite.
En plus d’offrir une plage de travail et une palette d’outils de mesure et d’annotation, Toutenclic, ouvre une fenêtre qui offre un choix de direction permettant à l’élève de cliquer sur une flèche de direction pour faire pivoter ou déplacer l’outil de mesure sélectionné. Cette fonction est particulièrement utile pour l’élève qui éprouve des difficultés marquées à déplacer son curseur dans l’écran.
Commentaires fermés sur Toutenclic
Publié dans Logiciels de surface
Mots-clés : annotation, géométrie, handicap, motricité, tracer
Résumé
Sankoré est un logiciel de surface offrant quelques outils de géométrie, pensé pour les Tableaux Blancs Interactifs (TBI), mais fonctionnant très bien avec une souris sur un poste traditionnel. Le logiciel fonctionne avec une photo d’écran de l’ordinateur. Sur cette image, on peut dessiner, écrire et manipuler des instruments de géométrie.
Tout comme Instrum’en poche, ce logiciel permet de réaliser des figures géométriques en exploitant des outils géométriques virtuels. Par défaut, le fond d’écran est une page blanche, mais d’autres fonds adaptés à l’apprentissage des mathématiques sont disponibles.
Installation du logiciel
Configuration nécessaire
Compatible avec : MacOS, Linux et Windows
Licence
Logiciel libre
Téléchargement
Site du logiciel : http://open-sankore.org/fr/
Vidéo
Construction d’un triangle équilatéral
Commentaires fermés sur Sankoré
Publié dans Logiciels de surface
Sauf indication contraire, le contenu de ce site est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les mêmes conditions 2.5 Canada.
