Voici une méthode mathématique simple de construction d’un carré.
1. Démarrer GeoGebra.
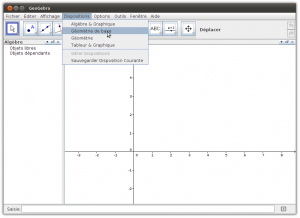
2. Dans le menu «Dispositions», sélectionner «Géométrie de base»
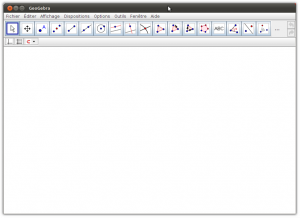
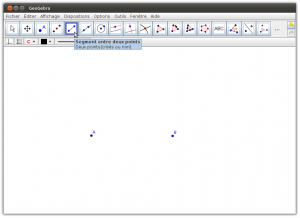
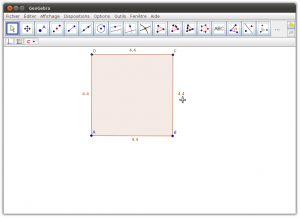
3. Vous obtenez la fenêtre ci-dessous
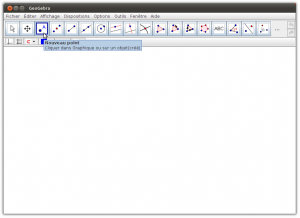
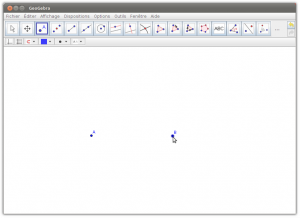
4. Créer deux points dans le plan
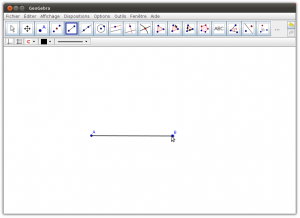
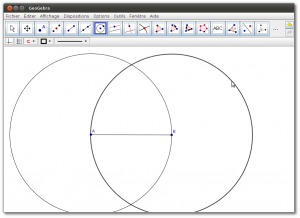
5. Créer un segment entre ces deux points
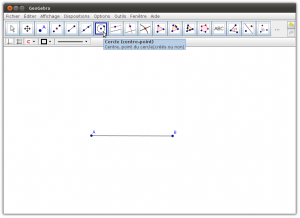
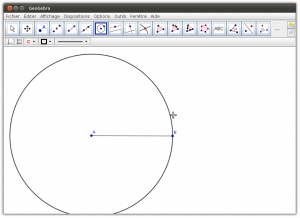
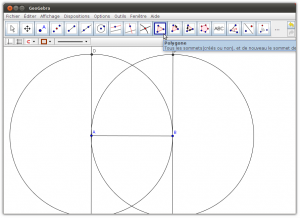
6. Créer un cercle de centre A et ayant comme extrémité de rayon B
7. Créer un cercle de centre B et ayant comme extrémité de rayon A
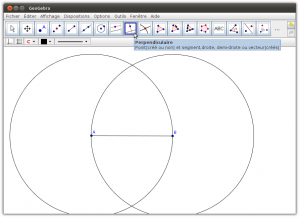
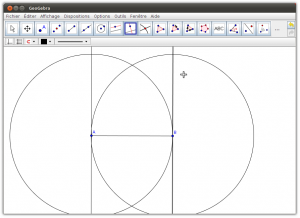
8. Tracer une droite perpendiculaire au segment AB passant par A
9. Tracer une droite perpendiculaire au segment AB passant par B
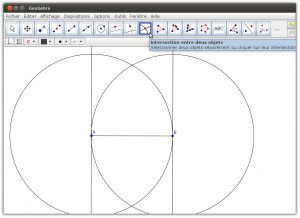
10. Créer un point d’intersection entre le cercle de centre A avec la perpendiculaire passant par A
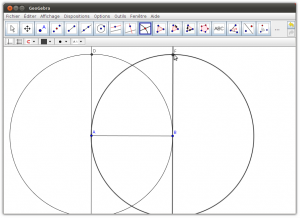
Cliquer sur le cercle de centre A et, par la suite, cliquer sur la perpendiculaire passant par A (deux points vont apparaître aux deux endroits où la perpendiculaire coupe le cercle A)
11. Créer un point d’intersection entre le cercle de centre B avec la perpendiculaire passant par B

Cliquer sur le cercle de centre B et, par la suite, cliquer sur la perpendiculaire passant par B (deux points vont apparaître aux deux endroits où la perpendiculaire coupe le cercle B)
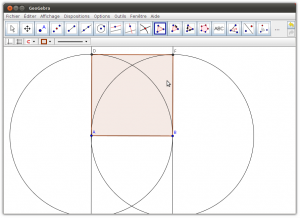
12. Créer un polygone en reliant les points A, B, D et F (il est possible que les points d’intersection ne se nomment pas D et F)
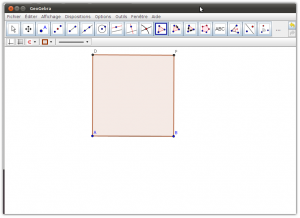
13. Cacher les traces de construction. Conserver seulement le polygone créé soit un carré.
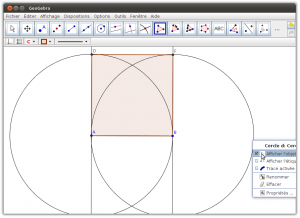
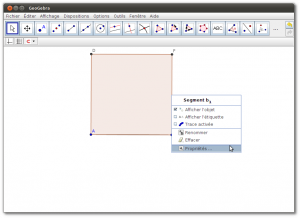
Cliquer le bouton droit sur l’objet à cacher. Cliquer sur «Afficher l’objet» afin d’enlever le crochet
Cacher tous les objets sauf le polygone.
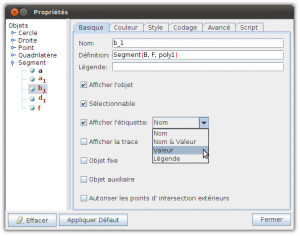
14. Faire afficher la mesure des segments composant le polygone.
15 Faire afficher la mesure des angles internes.
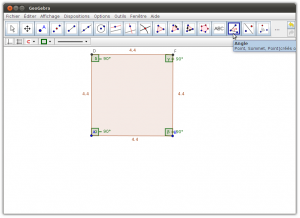
Cliquer sur l’outil «Angle» et cliquer à l’intérieur de votre polygone. La mesure des angles s’affichera.
Nous avons maintenant un véritable carré au sens mathématique du terme. En déplaçant les points A et B, le polygone créé conserve ses propriétés. Afin d’en connaître un peu plus sur le carré, visitez Wikipédia.